Elasticity
Algorithms for solving the 2D and 3D static linear elasticity equations
Problem
Solve:
$ \displaystyle{ -\nabla\cdot\sigma = \mathbf{f} } $
With:
$ \displaystyle{ \sigma_{ij}(\mathbf{u}) = \lambda\delta_{ij}\nabla\cdot\mathbf{u} + 2\mu\varepsilon_{ij}(\mathbf{u}) } $
and
$ \displaystyle{ \mu = \frac{E}{2(1+\nu)} ;\ \lambda = \frac{E\nu}{(1+\nu)(1-2\nu)} } $
Variational form
Let $\Omega\in\mathbb{R}^n$, $2\leq n\leq3$. Let $\mathbf{u}, \mathbf{v}\in \left(H^1(\Omega)\right)^n$. The variational form reads as follows:
$ \displaystyle{ \int_{\Omega}{\lambda\nabla\cdot\mathbf{u}\nabla\cdot\mathbf{v} + 2\mu\varepsilon(\mathbf{u})}:\varepsilon(\mathbf{v}) - \int_{\Omega}{\mathbf{f}\cdot\mathbf{v}} = 0 } $
Algorithms
2D
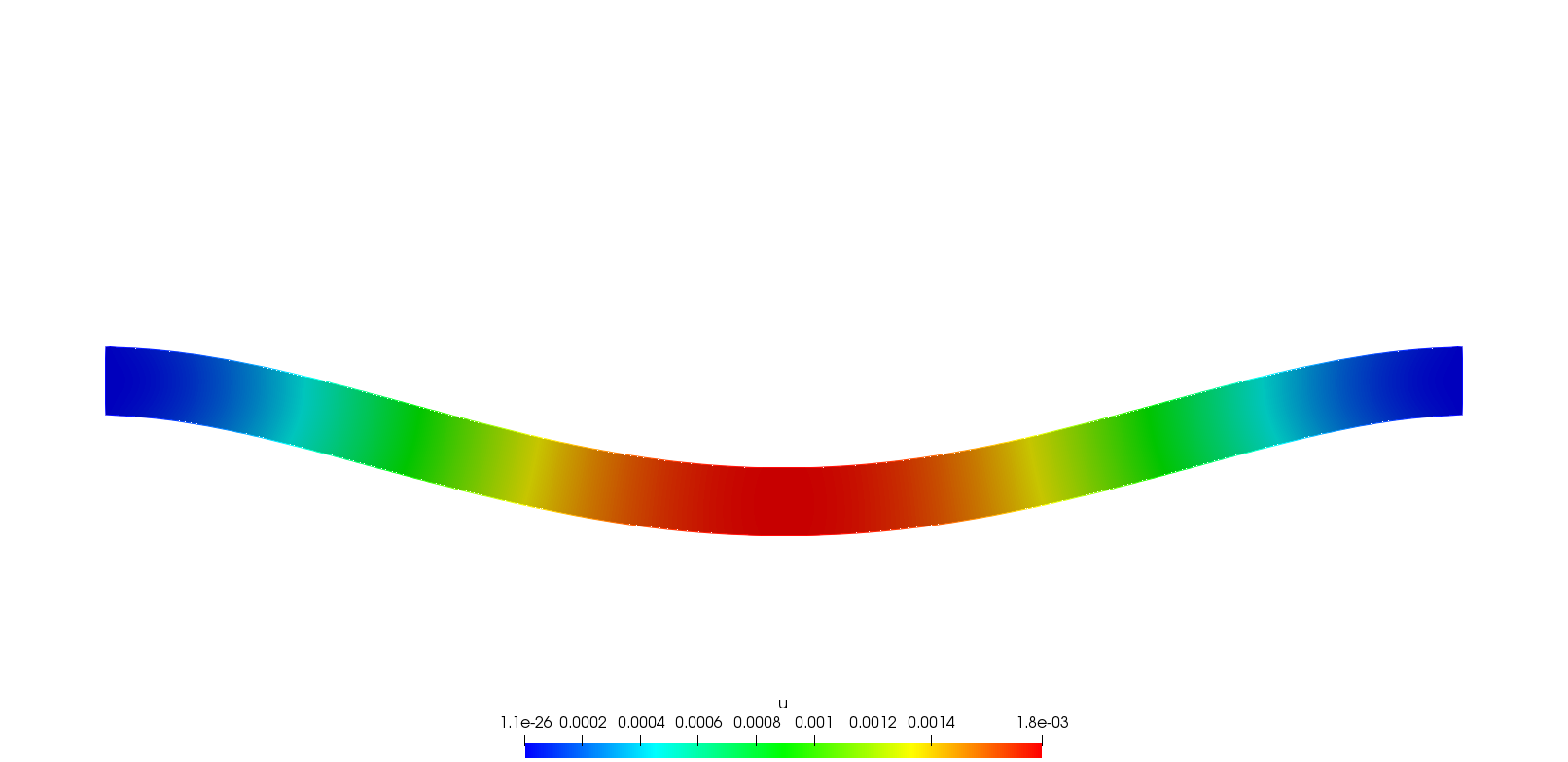
Elasticity equation on a beam.
//Parameters
real Rho = 8000.; //Density
real E = 210.e9; //Young modulus
real Nu = 0.27; //Poisson ratio
real Gravity = -9.81; //Gravity
//Mesh
real nn = 10; //Mesh quality
real L = 20.; //Beam length
real H = 1.; //Beam height
int Fixed = 1; //Beam fixed label
int Free = 2; //Beam free label
border b1(t=0., L){x=t; y=0.; label=Free;};
border b2(t=0., H){x=L; y=t; label=Fixed;};
border b3(t=0., L){x=L-t; y=H; label=Free;};
border b4(t=0., H){x=0.; y=H-t; label=Fixed;};
int nnL = max(2., nn*L);
int nnH = max(2., nn*H);
mesh Th = buildmesh(b1(nnL) + b2(nnH) + b3(nnL) + b4(nnH));
//Fespace
func Pk = P2;
fespace Uh(Th, [Pk, Pk]);
Uh [ux, uy];
//Macro
real sqrt2 = sqrt(2.);
macro Epsilon(ux, uy) [dx(ux), dy(uy), (dy(ux)+dx(uy))/sqrt2] //
macro Divergence(ux, uy) (dx(ux) + dy(uy)) //
//Problem
real Mu = E/(2.*(1.+Nu));
real Lambda = E*Nu/((1.+ Nu)*(1.-2.*Nu));
varf vElasticity ([ux,uy], [vx, vy])
= int2d(Th)(
Lambda * Divergence(vx, vy) * Divergence(ux, uy)
+ 2. * Mu * (
Epsilon(vx, vy)' * Epsilon(ux, uy)
)
)
+ int2d(Th)(
Rho * Gravity * vy
)
+ on(Fixed, ux=0, uy=0)
;
matrix<real> Elasticity = vElasticity(Uh, Uh, solver=sparsesolver);
real[int] ElasticityBoundary = vElasticity(0, Uh);
ux[] = Elasticity^-1 * ElasticityBoundary;
//Movemesh
Th = movemesh(Th, [x+ux, y+uy]);
[ux, uy] = [ux, uy];
//Plot
plot([ux, uy], value=true, cmm="u");| Result warped by a factor 1000 |
|---|
 |
3D
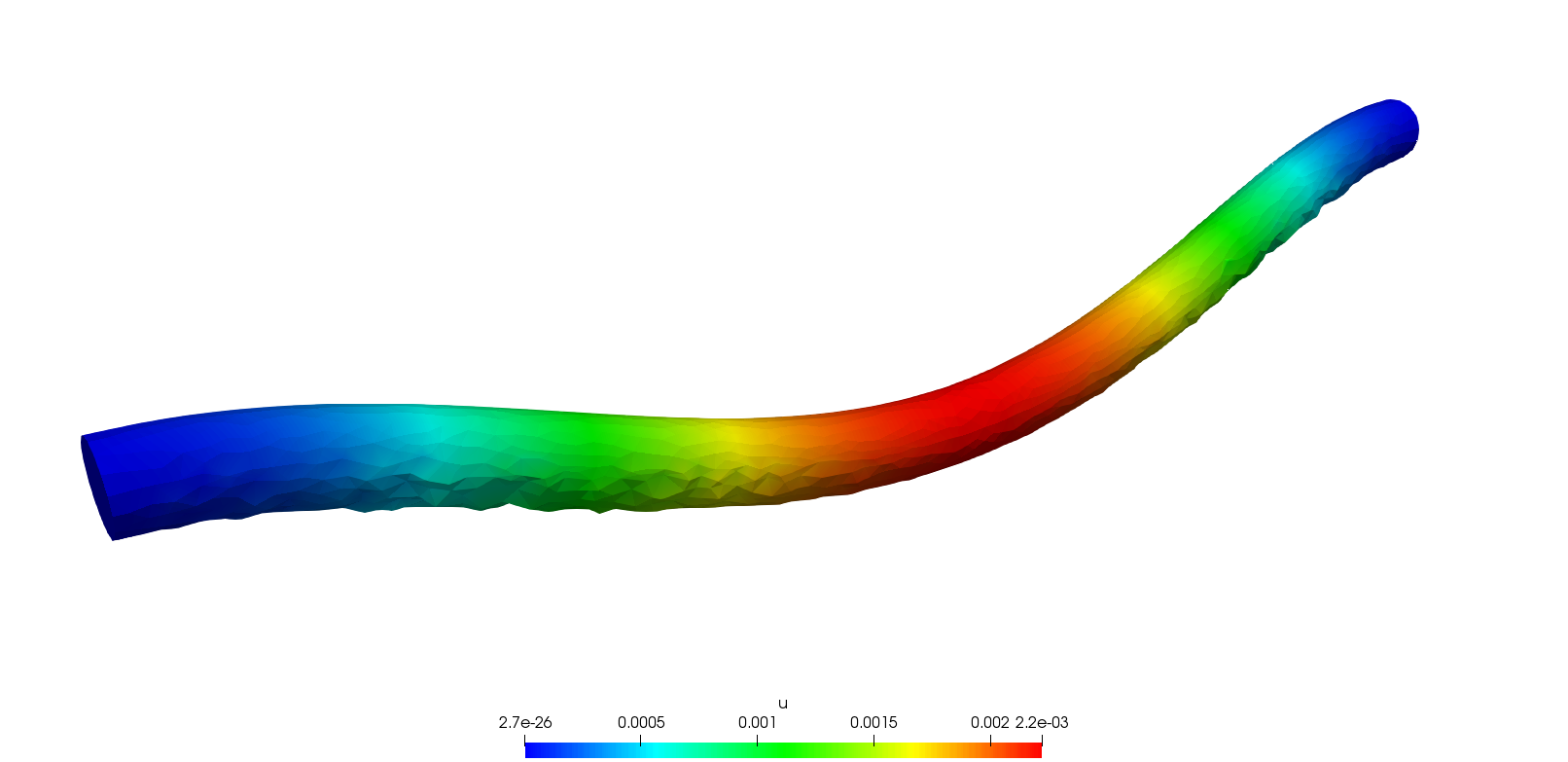
Elasticity equation on a beam.
load "gmsh"
load "msh3"
//Parameters
real Rho = 8000.; //Density
real E = 210.e9; //Young modulus
real Nu = 0.27; //Poisson ratio
real Gravity = -9.81; //Gravity
//Mesh
int Fixed = 1; //Beam fixed label
int Free = 2; //Beam free label
mesh3 Th = gmshload3("Elasticity3D.msh");
//Fespace
func Pk = P1;
fespace Uh(Th, [Pk, Pk, Pk]);
Uh [ux, uy, uz];
Uh [vx, vy, vz];
Uh [uxp, uyp, uzp];
Uh [uxpp, uypp, uzpp];
//Macro
real sqrt2 = sqrt(2.);
macro Epsilon(ux, uy, uz) [dx(ux), dy(uy), dz(uz),
(dz(uy)+dy(uz))/sqrt2,
(dz(ux)+dx(uz))/sqrt2,
(dy(ux)+dx(uy))/sqrt2] //
macro Divergence(ux, uy, uz) (dx(ux) + dy(uy) + dz(uz)) //
//Problem
real Mu = E/(2.*(1.+Nu));
real Lambda = E*Nu/((1.+Nu)*(1.-2.*Nu));
varf vElasticity ([ux, uy, uz], [vx, vy, vz])
= int3d(Th)(
Lambda * Divergence(vx, vy, vz) * Divergence(ux, uy, uz)
+ 2. * Mu * (
Epsilon(vx, vy, vz)' * Epsilon(ux, uy, uz)
)
)
+ int3d(Th)(
Rho * Gravity * vy
)
+ on(Fixed, ux=0, uy=0, uz=0)
;
matrix Elasticity = vElasticity(Uh, Uh, solver=sparsesolver);
real[int] ElasticityBoundary = vElasticity(0, Uh);
ux[] = Elasticity^-1 * ElasticityBoundary;
//Movemesh
Th = movemesh(Th, [x+ux, y+uy, z+uz]);
[ux, uy, uz] = [ux, uy, uz];
//Plot
plot([ux, uy, uz], value=true, cmm="u");| Result warped by a factor 1000 |
|---|
 |
Optional
Gmsh script:
Mesh.Optimize = 1;
////////////////
///PARAMETERS///
////////////////
h = 1./5.; //Mesh quality
L = 20.; //Beam length
D = 1.; //Beam height
Fixed = 1; //Beam fixed label
Free = 2; //Beam free label
////////////////
///ELEMENTARY///
////////////////
//Points
p = newp;
Point(p+0) = { 0., 0., 0.};
Point(p+1) = { D/2., 0., 0., h};
Point(p+2) = { 0., D/2., 0., h};
Point(p+3) = {-D/2., 0., 0., h};
Point(p+4) = { 0., -D/2., 0., h};
Point(p+5) = { 0., 0., L};
Point(p+6) = { D/2., 0., L, h};
Point(p+7) = { 0., D/2., L, h};
Point(p+8) = {-D/2., 0., L, h};
Point(p+9) = { 0., -D/2., L, h};
//Lines
l = newl;
Circle(l+0) = {p+1, p+0, p+2};
Circle(l+1) = {p+2, p+0, p+3};
Circle(l+2) = {p+3, p+0, p+4};
Circle(l+3) = {p+4, p+0, p+1};
Circle(l+4) = {p+6, p+5, p+7};
Circle(l+5) = {p+7, p+5, p+8};
Circle(l+6) = {p+8, p+5, p+9};
Circle(l+7) = {p+9, p+5, p+6};
Line(l+10) = {p+1, p+6};
Line(l+11) = {p+2, p+7};
Line(l+12) = {p+3, p+8};
Line(l+13) = {p+4, p+9};
//Line Loops
ll = newll;
Line Loop(ll+0) = {l+0, l+1, l+2, l+3};
Line Loop(ll+1) = {l+4, l+5, l+6, l+7};
Line Loop(ll+2) = {l+0, l+11, -(l+4), -(l+10)};
Line Loop(ll+3) = {l+1, l+12, -(l+5), -(l+11)};
Line Loop(ll+4) = {l+2, l+13, -(l+6), -(l+12)};
Line Loop(ll+5) = {l+3, l+10, -(l+7), -(l+13)};
//Surfaces
s = news;
Plane Surface(s+0) = {ll+0};
Plane Surface(s+1) = {ll+1};
Ruled Surface(s+2) = {ll+2};
Ruled Surface(s+3) = {ll+3};
Ruled Surface(s+4) = {ll+4};
Ruled Surface(s+5) = {ll+5};
//Surface loops
sl = newsl;
Surface Loop(sl+0) = {s+0, s+1, s+2, s+3, s+4, s+5};
//Volumes
v = newv;
Volume(v+0) = {sl+0};
//////////////
///PHYSICAL///
//////////////
//Surfaces
Physical Surface("Fixed", Fixed) = {s+0, s+1};
Physical Surface("Free", Free) = {s+2, s+3, s+4, s+5};
//Volumes
Physical Volume("Volume", 1) = {v+0};| Mesh |
|---|
 |
Validation
TODO
Authors
Author: Simon Garnotel
