Poisson

Algorithms for solving the 2D and 3D Poisson’s equation

Problem

Let $u\in\mathbb{R}$, solve:

$ -\displaystyle{\Delta u = f} $

With $f$ an external force.

Variational form

Let $\Omega\in\mathbb{R}^n$, $2\leq n\leq3$. Let $u, v\in H^1(\Omega)$. The variational form reads as follows:

$ \displaystyle{-\int_{\Omega}{\Delta u v} - \int_{\Omega}{f v} = 0} $

Using the Green formula:

$ \displaystyle{\int_{\Omega}{\nabla u \cdot \nabla v} - \int_{\Omega}{f v} = 0} $

Algorithms

2D

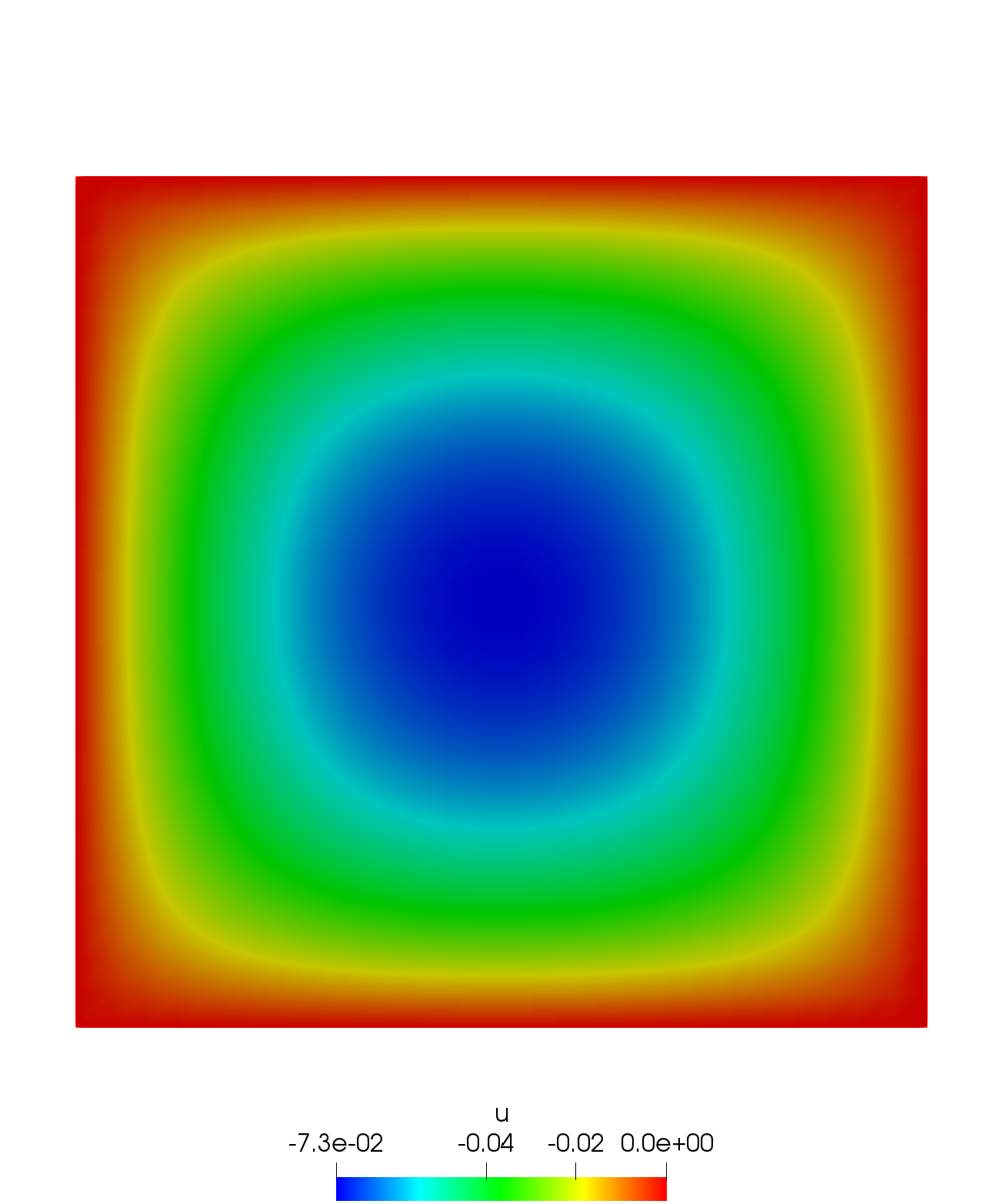
Poisson’s equation on a square.

// Parameters
func f = 1.;

// Mesh
int nn = 25;	//Mesh quality
mesh Th = square(nn, nn);

// Fespace
func Pk = P2;
fespace Uh(Th, Pk);
Uh u;

// Macro
macro grad(A) [dx(A), dy(A)] //

// Problem
varf vPoisson (u, uh)
	= int2d(Th)(
		  grad(u)' * grad(uh)
	)
	+ int2d(Th)(
		  f * uh
	)
	+ on(1, 2, 3, 4, u=0)
	;
matrix<real> Poisson = vPoisson(Uh, Uh, solver=sparsesolver);
real[int] PoissonBoundary = vPoisson(0, Uh);
u[] = Poisson^-1 * PoissonBoundary;

// Plot
plot(u, nbiso=30, fill=true, value=true, cmm="A");
Result
Result

3D

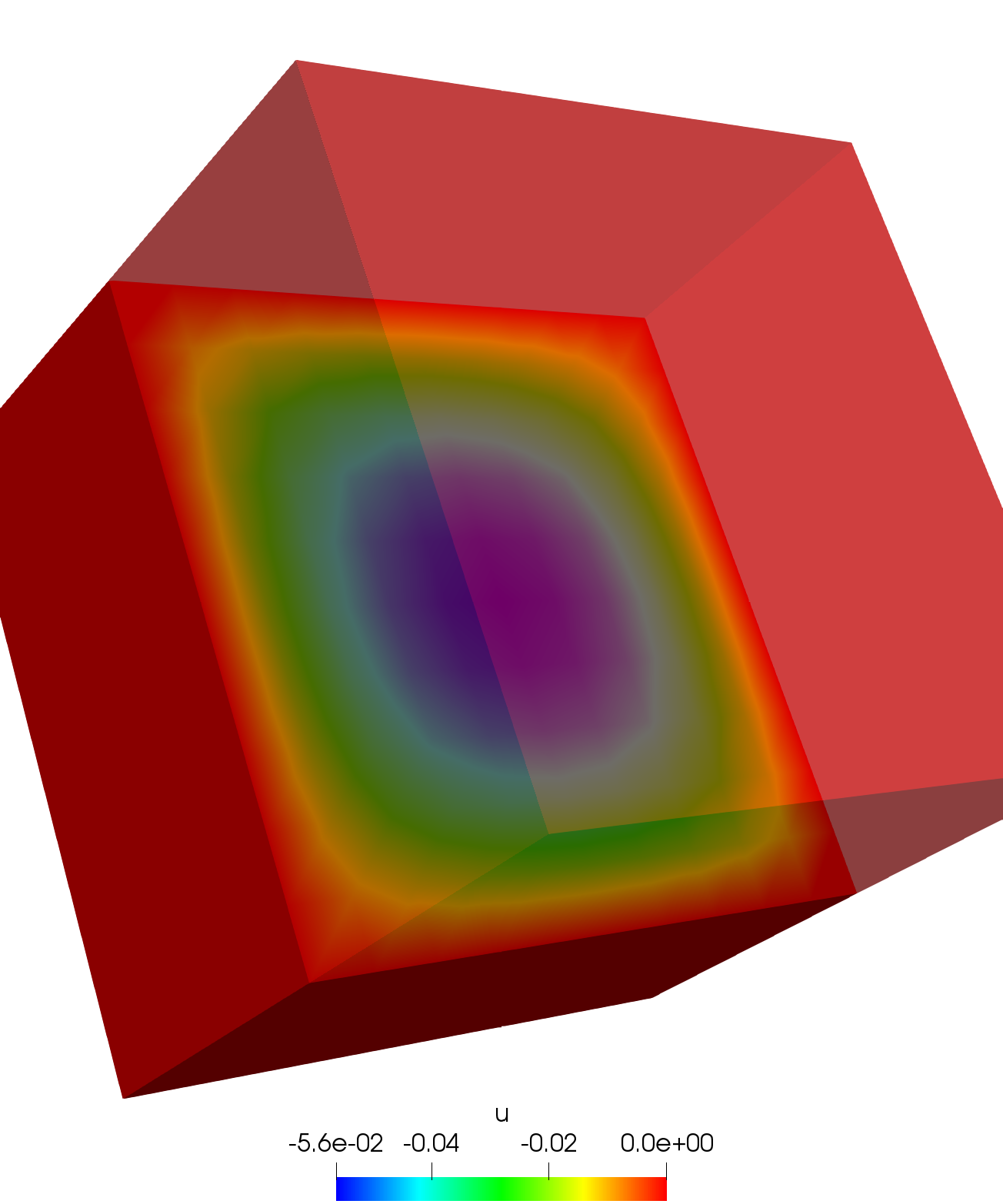
Poisson’s equation on a cube.

include "cube.idp"

// Parameters
func f = 1.;

// Mesh
int nn = 10;
mesh3 Th = cube(nn, nn, nn);

// Fespace
func Pk = P2;
fespace Uh(Th, Pk);
Uh u;

// Macro
macro grad(A) [dx(A), dy(A), dz(A)] //

// Problem
varf vPoisson (u, uh)
	= int3d(Th)(
		  grad(u)' * grad(uh)
	)
	+ int3d(Th)(
		  f * uh
	)
	+ on(1, 2, 3, 4, 5, 6, u=0)
	;
matrix<real> Poisson = vPoisson(Uh, Uh, solver=sparsesolver);
real[int] PoissonBoundary = vPoisson(0, Uh);
u[] = Poisson^-1 * PoissonBoundary;

// Plot
plot(u, nbiso=30, fill=true, value=true, cmm="A");
Result
Result

Validation

2D

Let $u_e$ be the analytical solution on $\Omega=[0,1]^2$:

$ \displaystyle{ u_e = x(1-x)y(1-y)e^{x-y} } $

We get, for homogenous Dirichlet conditions on $\partial\Omega$:

$ \displaystyle{ f = -2x(y-1)(y-2x+xy+2)e^{x-y} } $

and the following convergence curve:

Convergence curve
Convergence curve

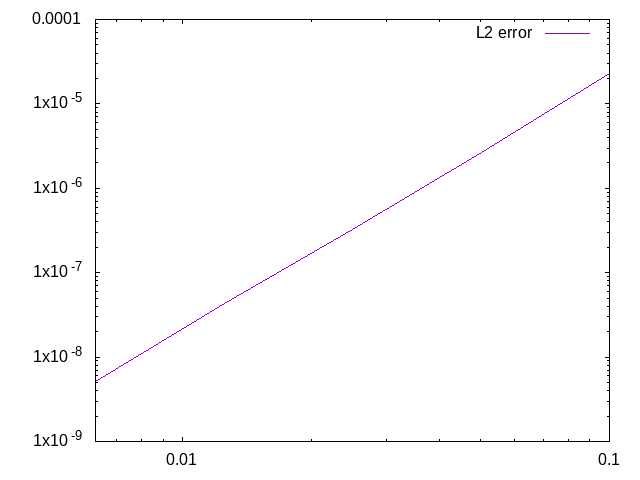The slope obtained with this algorithm is equal to $3.0235$, which corresponds to the theoretical value of $3$.

The complete validation script is available here

Authors

Author: Simon Garnotel