Helmoltz
Algorithms for solving the 2D Helmoltz equation.
Problem
Solve:
$ \displaystyle{todo} $
Variational form
$ \displaystyle{ todo } $
Algorithms
2D
load "ffrandom"
// RandInit
srandomdev();
// Parameters
int n = 13;
real a = 40;
real b = 40;
real c = 0.5;
func Pk = P2;
// Mesh
border a00(t=0,1) {x=a*t; y=0; label=1;}
border a10(t=0,1) {x=a; y=b*t; label=1;}
border a20(t=1,0) {x=a*t; y=b; label=1;}
border a30(t=1,0) {x=0; y=b*t; label=1;}
border a01(t=0,1) {x=c+(a-c*2)*t; y=c; label=1;}
border a11(t=0,1) {x=a-c; y=c+(b-c*2)*t; label=1;}
border a21(t=1,0) {x=c+(a-c*2)*t; y=b-c; label=1;}
border a31(t=1,0) {x=c; y=c+(b-c*2)*t; label=1;}
real p=5, q=20, d=34, e=1;
border b00(t=0,1) {x=p+d*t; y=q; label=3;}
border b10(t=0,1) {x=p+d; y=q+e*t; label=3;}
border b20(t=1,0) {x=p+d*t; y=q+e; label=3;}
border b30(t=1,0) {x=p; y=q+e*t; label=3;}
real r=30, s=1, j=1, u=15;
border c00(t=0,1) {x=r+j*t; y=s; label=3;}
border c10(t=0,1) {x=r+j; y=s+u*t; label=3;}
border c20(t=1,0) {x=r+j*t; y=s+u; label=3;}
border c30(t=1,0) {x=r; y=s+u*t; label=3;}
mesh Sh = buildmesh(a00(10*n)+a10(10*n)+a20(10*n)+a30(10*n)
+a01(10*n)+a11(10*n)+a21(10*n)+a31(10*n)
+b00(5*n)+b10(5*n)+b20(5*n)+b30(5*n)
+c00(5*n)+c10(5*n)+c20(5*n)+c30(5*n));
plot(Sh);
// Source loop
for (int bx = 1; bx <= 7; bx++){
border C(t=0,2*pi){x=2+cos(t);y=bx*5+sin(t);label=2;}
mesh Th = buildmesh(a00(10*n)+a10(10*n)+a20(10*n)+a30(10*n)
+a01(10*n)+a11(10*n)+a21(10*n)+a31(10*n)+C(10)
+b00(5*n)+b10(5*n)+b20(5*n)+b30(5*n)
+c00(5*n)+c10(5*n)+c20(5*n)+c30(5*n));
// Fespace
fespace Vh(Th, Pk);
Vh wallreflexion = randreal1();
Vh<complex> wallabsorption = randreal1()*0.5i;
Vh k = 6;
Vh<complex> v, w;
// Function
func real wall(){
if (Th(x,y).region == Th(0.5,0.5).region || Th(x,y).region == Th(7,20.5).region || Th(x,y).region == Th(30.5,2).region)
return 1;
else
return 0;
}
cout << "Reflexion of walls : " << wallreflexion[].max << "\n";
cout << "Absorption of walls : " << wallabsorption[].max << "\n";
// Problem
problem muwave(v, w)
= int2d(Th)(
(v*w*k^2)/(1+(wallreflexion+wallabsorption)*wall())^2
- (dx(v)*dx(w)+dy(v)*dy(w))
)
+ on(2, v=1)
;
// Solve
muwave;
// Plot
Vh vm = log(real(v)^2 + imag(v)^2);
plot(vm, fill=true, value=false, nbiso=65);
}| Result |
|---|
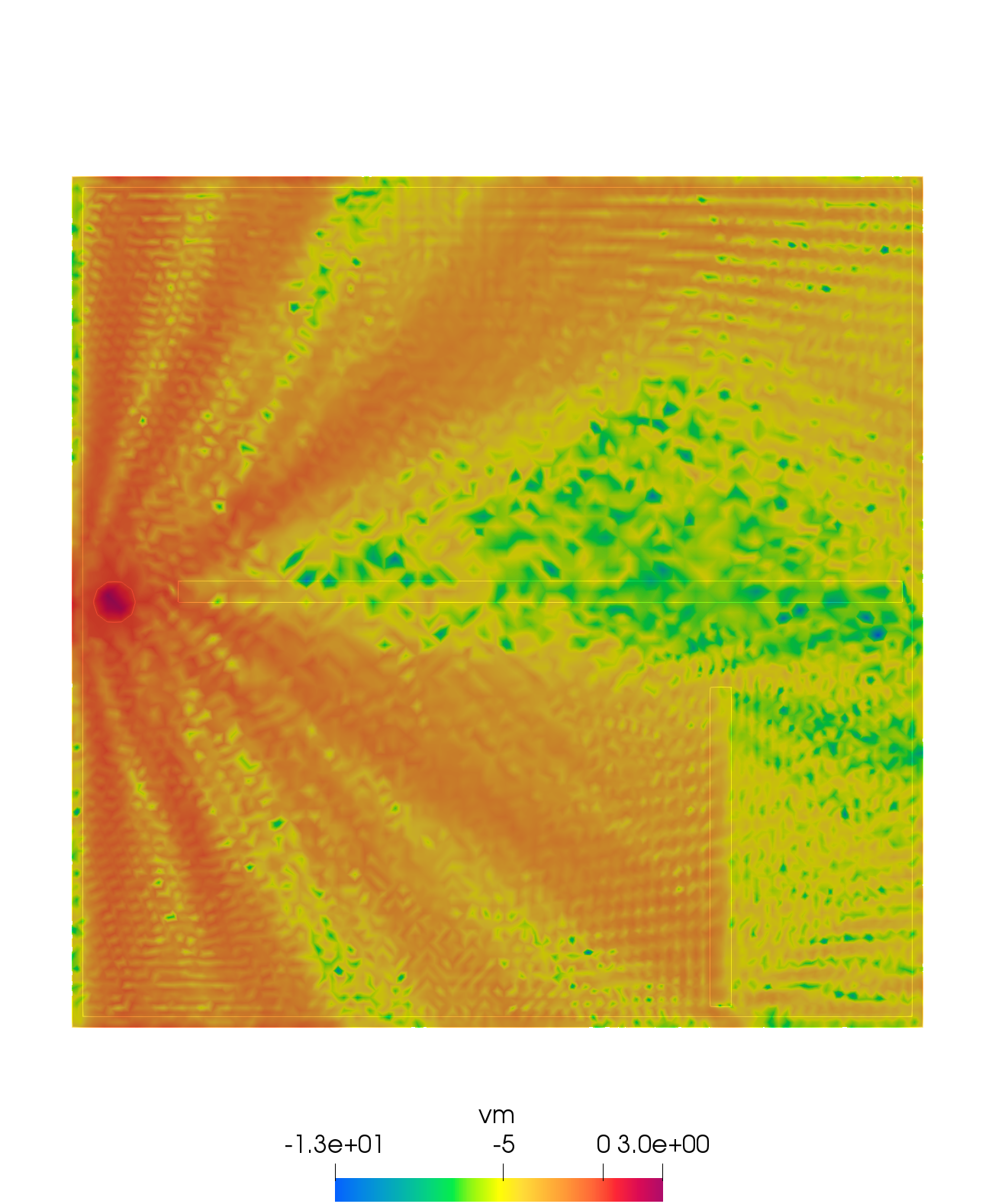 |
Authors
Author: Alexis Tacnet
