Elasticity solid
Helmoltz electromagnetism
Magnetostatic electromagnetism
Maxwell waveguide boundary conditions electromagnetism, academic
Navier-Stokes characteristics fluid
Signorini’s contact mechanics, validated
Non-linear elasticity mechanics, validated
Piezoelectricity solid
Poisson academic, validated
Steady Navier-Stokes fluid
Stokes fluid
3D meshing example academic, electromagnetism
Wentzell academic

Maxwell waveguide boundary conditions

This module illustrates how to implement waveguide boundary conditions in Maxwell equations. So far it is done for 2D planar case in Cartezian and Axial (m = 0) cases. Waveguides modes and waveguides port are hardcoded.

Problem

The module uses Maxwell equations written for $\mathbf{E}$ field in $\exp(-i \omega t)$ presentation: $curl curl \mathbf{E} = \frac{\omega^2}{c^2} \epsilon(x,y) \mathbf{E}$ (here: $\omega$ - is the frequency, $c$ - the speed of light, $\epsilon$ - dielectric permittivity; the CGS system of units is used).

This module illustrates how to set boundary condition so that there is two waveguide ports through one of which an input signal enters. That is it solves a simple waveguide scattering problem

Variational form

Variational form is:

\[\int_V dV ( curl(\mathbf{E}) curl(\mathbf{V}) - \frac{\omega^2}{c^2} \epsilon(x,y) \mathbf{E} \mathbf{V}) + \int_{dV} dS curl (\mathbf{E}) \mathbf{V} = 0\]

For waveguide ports the last term in the left hand side is written as:

\[\int_{dS_{port}} curl \mathbf{E} \mathbf{V} = \sum_{s=1,N_{modes}} C_s \int_{dS} curl \mathbf{E_s} \mathbf{V}\]

Here C_s is the amplitude of mode $s$ and $\mathbf(E_s)$ - the s-th mode’s electric field. The $C_s$ in its turn is written as:

\[C_s = \frac{1}{N_s} \int_{S_{port}} dS ( \mathbf{E} \times \mathbf{H_s} - \mathbf{E_s} \times \mathbf{H})\]

, here $\mathbf{H}$ and $\mathbf{H_s}$ are current and mode’s magnetic field which are found from Maxwell equations, $N_s$ is the norm.

Finally, the last term of the LHS side can be written in term of the direct product as:

\[\int_{dS_{port}} curl \mathbf{E} \mathbf{V} = \sum_{s=1,N_{modes}} \frac{1}{N_s} \int_{S_{port}} dS ( \mathbf{E} \times \mathbf{H_s} - \mathbf{E_s} \times \mathbf{H}) \bigotimes \int_{dS} curl \mathbf{E_s} \mathbf{V},\]

that allows one to implement it by means of FreeFEM tools without low-level matrix assembly (for the price of performance, of course).

Algorithms

2D - Cartesian

Hardcoded TE modes. File cartezian2D_TEmodes.idp:

// cartezian2D_TEmodes.idp
func real Kappate(int modeNumber, real size1, real size2)
{
    return pi*modeNumber/size1;
}
func complex anEte(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    real kp = Kappate(abs(modeNumber), size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(componentNumber == 3){
        return -sin(kp*yy)*(1. + 0*1i)*sqrt(k/h)*exp(1i*h*xx*sign);
    }
    return 0*1i;
}

func complex anHte(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    real kp = Kappate(abs(modeNumber), size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(componentNumber == 3){
        return 0;
    }
    if(componentNumber == 2){
        return -sin(kp*yy)*sqrt(h/k)*sign*exp(1i*h*xx*sign);
    }
    if(componentNumber == 1){
        return  kp*cos(kp*yy)/(1i*k)*sqrt(k/h)*exp(1i*h*xx*sign);
    }    
    return 0*1i;
}

func real fNormte(int modeNumber, real size1)
{
    return  1.*size1;
}

Hardcoded TM modes. File cartezian2D_TMmodes.idp

// cartezian2D_TMmodes.idp
func real Kappatm(int modeNumber, real size1, real size2)
{
    return pi*(modeNumber-1)/size1;
}
func complex anHtm(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    real kp = Kappatm(abs(modeNumber), size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(componentNumber == 3){
        return cos(kp*yy)*sqrt(k/h)*exp(1i*h*xx*sign);
    }
    return 0;
}

func complex anEtm(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    real kp = Kappatm(abs(modeNumber), size1, 0);
    real h = H(k, kp);    
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(componentNumber == 3){
        return 0;
    }
    if(componentNumber == 2){
        return cos(kp*yy)*sqrt(h/k)*exp(1i*h*xx*sign)*sign;
    }    
    if(componentNumber == 1){
        return  kp*sin(kp*yy)/(1i*sqrt(k*h))*exp(1i*h*xx*sign);
    }    
    return 0*1i;
}

func real fNormtm(int modeNumber, real size1)
{
    if(abs(modeNumber) == 1) return 2.*size1;
    else return  1.*size1;
}

Script for intermixing TM and TE modes. File cartezian2D_modes.idp:

// cartezian2D_modes.idp
func real H(real k, real kp)
{
    return sqrt(k*k-kp*kp);
}
include "cartezian2D_TEmodes.idp"
include "cartezian2D_TMmodes.idp"
func complex anE(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(abs(modeNumber) % 2 == 0)
        return anEte(xx, yy, abs(modeNumber)/2*sign, componentNumber, size1, size2, k);
    else
        return anEtm(xx, yy, (modeNumber+sign*1)/2, componentNumber, size1, size2, k);
}
func complex anH(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(abs(modeNumber) % 2 == 0)
        return anHte(xx, yy,  abs(modeNumber)/2*sign, componentNumber, size1, size2, k);
    else
        return anHtm(xx, yy, (modeNumber+sign*1)/2, componentNumber, size1, size2, k);
}
func real fNorm(int modeNumber, real size1)
{
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(abs(modeNumber) % 2 == 0)
        return fNormte( abs(modeNumber)/2*sign, size1);
    else
        return fNormtm((modeNumber+sign*1)/2, size1);
}
func real Kappa(int modeNumber, real size1, real size2)
{
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    if(modeNumber % 2 == 0)
        return Kappate(modeNumber/2, size1, 0);
    else
        return Kappatm((modeNumber+1)/2, size1, 0);
}

Finally, the main script:

load "Element_Mixte"
func complex epsilon(real xx, real yy)
{
     return 1. + 0*1i;
//    if(xx > 0.25 && xx < 0.75/* && yy > 0.25 && yy < 0.75*/) return 5;
//    else return  1.;
}
include "cartezian2D_modes.idp"
//include "cartezian2D_TE_only.idp"
//include "cartezian2D_TM_only.idp"

real height = 1;
real length = 2;
func mesh generateMesh()
{
    return square(50,10, [x*length, y*height]);
}
int rightBorderLabel = 2;
int  leftBorderLabel = 4;
mesh Th = generateMesh();
plot(Th);

fespace Vh(Th,[RT1Ortho, P2]); // finite element space

func matrix<complex> MakswellEqs(real sigma, int m)
{       
   varf MKSWL([Ex,Ey, Ez],[vEx, vEy, vEz]) =
        int2d(Th)(
    (
         (dy(Ez) - 1i*m*Ey )*conj(dy(vEz)- 1i*m*vEy )       //curl_x
     +   (dx(Ey) - dy(Ex))*conj(dx(vEy) - dy(vEx))          //curl_z
     +   (1i*m*Ex  - dx(Ez))*conj(1i*m*vEx  - dx(vEz))      //curl_y

    )
    -sigma*epsilon(x,y)*(conj(vEy)*Ey+conj(vEz)*Ez + conj(vEx)*Ex)
                )
        + on(1, 3, Ex = 0, Ey = 0, Ez = 0)
     ;
    matrix<complex> OP = MKSWL(Vh, Vh, solver=UMFPACK);
    return OP;
}  

func complex[int] vectorBCh(int modeNum, int boundaryLabel, real k)
{
    varf BoundCondRot([Ex,Ey,Ez],[vEx,vEy,vEz]) =
        int1d(Th,boundaryLabel)(          
        (
            anH(x, y, (N.x)*modeNum, 1, height, 0, k)*conj(0*vEy - N.y*vEz)
          + anH(x, y, (N.x)*modeNum, 2, height, 0, k)*conj(N.x*vEz - 0*vEx)
          + anH(x, y, (N.x)*modeNum, 3, height, 0, k)*conj(N.y*vEx - N.x*vEy)
        )*(1i*k)                    // [n v*] curl E = [n v*] (i k H)               
                                );                         
    complex[int] BCr = BoundCondRot(0,Vh);
    return BCr;                

}    

func complex[int] vectorBCe(int modeNum, int boundaryLabel, real k)
{
    varf BoundCondField([Ex,Ey,Ez],[vEx,vEy,vEz]) =
        int1d(Th,boundaryLabel)
        (
            (conj(
                  - vEz*anH(x, y, (N.x)*modeNum, 2, height, 0, k)        
                  - anE(x, y,  (N.x)*modeNum, 3, height, 0, k)*(dx(vEz)/(1i*k) )
                  + vEy *anH(x, y,  (N.x)*modeNum, 3, height, 0, k)
                  - anE(x, y,  (N.x)*modeNum, 2, height, 0, k)*((dx(vEy) - dy(vEx))/(1i*k))
                  )*(N.x)
            )
            /fNorm(modeNum, height)
        );
    complex[int] BCrf = BoundCondField(0,Vh);
    return BCrf;

}
func matrix<complex> matrixBC(int modeNum, int boundaryLabel, real k)
{        
    complex[int] BCr  = vectorBCh( modeNum, boundaryLabel,k);
    complex[int] BCrf = vectorBCe( -modeNum, boundaryLabel,k);
    matrix<complex> Br = BCr*BCrf'; // 'cartesian product
    return Br;        
}    

func matrix<complex> generateBCMatrix(int numberOfModes, int boundaryLabel, int sign, real k)
{
    matrix<complex> Br1;
    for(int i = 1; i <= numberOfModes; i++)
    {
        matrix<complex> Br2 = matrixBC(sign*i, boundaryLabel, k);
        Br1 = Br1 + Br2;
    }
    return Br1;        
}    
func complex[int] modeAmplitudes
(complex[int]& eVec, int numOfModes, int referenceMode, int inputBoundaryLabel, int otherBoundaryLabel, real k,  bool needdB)
{
    complex[int] result(numOfModes);
    Vh<complex> [ex,ey,ez];
    ex[] = eVec;
    if(needdB) for(int i = 0; i < numOfModes; i++) result(i) = log10(0.);
    complex[int] probe = vectorBCe( -referenceMode, inputBoundaryLabel, k);
    complex power = eVec'*probe;     //'
    cout<<"mode = "<<referenceMode<<"   power = "<<abs(power)<<", "<<power<<endl;
    for(int testmode = 0; testmode < numOfModes; testmode++)             
    {
        // complex[int] probe2 = vectorBCe( (testmode+1), otherBoundaryLabel);
        // complex res = eVec'*probe2/power;   //'
        complex res = int1d(Th,otherBoundaryLabel)
        (
            (
                conj(
                    - ez*anH(x, y, -(N.x)*(testmode+1), 2, height, 0, k)
                    - anE(x, y, -(N.x)*(testmode+1), 3, height, 0, k)*(dx(ez)/(1i*k) )
                    + ey*anH(x, y, -(N.x)*(testmode+1), 3, height, 0, k)
                    - anE(x, y, -(N.x)*(testmode+1), 2, height, 0, k)*((dx(ey) - dy(ex))/(1i*k))
                    )*(N.x)
            )
            /(fNorm(-(N.x)*(testmode+1), height)*power)
        );
         if(needdB) result(testmode) =  20*log10(abs(res));
         else       result(testmode) =  res;
    }
    return result;
}

real sigma = 9.*pi*pi+3.;
real k = sqrt(sigma);
cout<<"h1 = "<<H(k, Kappa(1,1,1))<<",  kappa1 = "<<Kappa(1,1,1)<<endl;
cout<<"h2 = "<<H(k, Kappa(2,1,1))<<",  kappa2 = "<<Kappa(2,1,1)<<endl;
cout<<"h3 = "<<H(k, Kappa(3,1,1))<<",  kappa3 = "<<Kappa(3,1,1)<<endl;
cout<<"h4 = "<<H(k, Kappa(4,1,1))<<",  kappa4 = "<<Kappa(4,1,1)<<endl;     

int numberOfModesToAccount = 4;
matrix<complex> Br = generateBCMatrix(numberOfModesToAccount, rightBorderLabel,1, k);
matrix<complex> Bl = generateBCMatrix(numberOfModesToAccount, leftBorderLabel, 1, k);
matrix<complex> OP = MakswellEqs(sigma, 0) ;

matrix<complex> A; //A = OP + generateBCMatrix(...) + generateBCMatrix(...) produces order dependent incorrect result
A = OP;            //tested FreeFem++ v 3.56
A = A + Br;        
A = A + Bl;                                                 
complex[int] u(Bl.n);
set(A, solver = UMFPACK);
complex[int] RHS =  vectorBCh(2 , leftBorderLabel, k);    

u = A^-1*(RHS);

Vh<complex> [Ex,Ey,Ez];
Ex[] = u;

// plot(Ex, fill = true, cmm = "Ex");
plot(Ey, fill = true, cmm = "Ey");
plot(Ez, fill = true, cmm = "Ez");

cout<<    modeAmplitudes(u, numberOfModesToAccount, -2, leftBorderLabel,  leftBorderLabel, k, true)<<endl;
cout<<    modeAmplitudes(u, numberOfModesToAccount, -2, leftBorderLabel, rightBorderLabel, k, true)<<endl;

2D - axial-symmetric

In the axial-symmetric case dimensionless norm and transversal wave numbers are read from file modes_m=0.txt. If only TE or TM modes are required, just delete unnecessary raws. The first lines is the lines number. For the rest: the first column is Bessel funstion or Bessel function prime zeros, the second column is the mode type (TE or TM), the next is M=0, the last is the dimensionless norm. modes_m=0.txt:

19
404825557695773	1 	0	0.7793251491983979
8317059702075125	0 	0	1.190818894252844
5200781102863115	1 	0	1.763983488461943
0155866698156215	0 	0	2.2165400124021
653727912911013	1 	0	2.7590751389668657
173468135062722	0 	0	3.226726175661221
791534439014281	1 	0	3.7566997735908174
323691936314221	0 	0	4.232168817077737
930917708487787	1 	0	4.755305323217033
470630050877634	0 	0	5.235551752495418
071063967910924	1 	0	5.754389740203993
615858510468243	0 	0	6.237857058819471
21163662987926	1 	0	6.753743000677423
760084380592772	0 	0	7.239528520160257
352471530749302	1 	0	7.753262043197564
903672087618382	0 	0	8.240795797022049
493479132040253	1 	0	8.752890449018484
046828534916855	0 	0	9.241789609116804
634606468431976	1 	0	9.752594764648169

Hardcoded TE modes, file axial2D_TEmodes.idp:

//axial2D_TEmodes.idp
func real Kappate(int modeNumber, real size1, real size2)
{
    return kappas[abs(modeNumber)-1]/size1;
}
func complex anEte(real xx, real yy, int modeNumber, int M, int componentNumber, real size1, real size2, real k)
{
    if(M!=0){ cout<< "M != 0: feature not implemented" <<endl; exit(-1);}
    real kp = Kappate(modeNumber, size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    real rho = kp*yy;
    real mu = kp*size1;
    //cout << kp << "," << h << "," << rho << endl;
    int m = M*sign;
    if(componentNumber == 2){ //r
        return 0;                   //  k*m*jn(M, rho)*exp(1i*h*xx*sign)/yy; // m == 0
    }
    if(componentNumber == 3){//phi    
        real jnDash = 0.5*(jn(M-1, rho) - jn(M+1, rho));        
        return 1i*k*mu*(jnDash)*exp(1i*h*xx*sign)/size1;
    }
    return 0*1i;
}

func complex anHte(real xx, real yy, int modeNumber, int M,  int componentNumber, real size1, real size2, real k)
{
    if(M!=0){ cout<< "M != 0: feature not implemented" <<endl; exit(-1);}
    real kp = Kappate(abs(modeNumber), size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    real rho = kp*yy;
    real mu = kp*size1;
    real m = M*sign;    
    if(componentNumber == 3){//phi
        return 0; // h*m*sign*jn(M, rho)*exp(1i*h*xx*sign);  // m == 0
    }
    if(componentNumber == 2){//r
        real jnDash = 0.5*(jn(M-1, rho) - jn(M+1, rho));
	return -1i*h*sign*mu*jnDash/size1*exp(1i*h*xx*sign);
    }
    if(componentNumber == 1){//z
        return  (-k*k + h*h)*jn(M, rho)*exp(1i*h*xx*sign);
    }    
    return 0*1i;
}

func real fNormte(int modeNumber, real size1, real k)
{
    real kp = Kappate(modeNumber, size1, 0);
    real h = H(k, kp);
    return  4.*pi*h*k*norma[abs(modeNumber)-1];
}

Hardcoded TM modes, file axial2D_TMmodes.idp:

func real Kappatm(int modeNumber, real size1, real size2)
{
    return kappas[abs(modeNumber)-1]/size1;
}
func complex anHtm(real xx, real yy, int modeNumber, int M, int componentNumber, real size1, real size2, real k)
{
    if(M!=0){ cout<< "M != 0: feature not implemented" <<endl; exit(-1);}
    real kp = Kappatm(modeNumber, size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    real rho = kp*yy;
    real mu = kp*size1;
    int m = M*sign;
    if(componentNumber == 2){ //r
        return 0;   //-k*m*jn(M, rho)*exp(1i*h*xx*sign)/yy;   // m == 0
    }
    if(componentNumber == 3){//phi    
        real jnDash = 0.5*(jn(M-1, rho) - jn(M+1, rho));        
        return -1i*k*mu*(jnDash)*exp(1i*h*xx*sign)/size1;
    }
    return 0*1i;
}

func complex anEtm(real xx, real yy, int modeNumber, int M,  int componentNumber, real size1, real size2, real k)
{
    if(M!=0){ cout<< "M != 0: feature not implemented" <<endl; exit(-1);}
    real kp = Kappatm(abs(modeNumber), size1, 0);
    real h = H(k, kp);
    real sign = 0; if(modeNumber >= 0) sign = 1.; else sign = -1.;
    real rho = kp*yy;
    real mu = kp*size1;
    real m = M*sign;    
    if(componentNumber == 3){//phi
        return 0;      // h*m*sign*jn(M, rho)*exp(1i*h*xx*sign)/(yy); // m == 0
    }
    if(componentNumber == 2){//r
        real jnDash = 0.5*(jn(M-1, rho) - jn(M+1, rho));
        return -1i*h*sign*mu*jnDash/size1*exp(1i*h*xx*sign);
    }
    if(componentNumber == 1){//z
        return  (-k*k + h*h)*jn(M, rho)*exp(1i*h*xx*sign);
    }    
    return 0*1i;
}
func real fNormtm(int modeNumber, real size1, real k)
{
    real kp = Kappatm(modeNumber, size1, 0);
    real h = H(k, kp);
    return  -4*pi*h*k*norma[abs(modeNumber)-1];
}

Script for intermixing TM and TE modes. File axial2D_modes.idp:

// axial2D_modes.idp
ifstream modeInput("modes_m=0.txt");
int modesNumInput;
modeInput >> modesNumInput;
real[int] kappas(modesNumInput);
int[int] modeType(modesNumInput);
int[int] modeM (modesNumInput);
real[int] norma(modesNumInput);
for(int i = 0; i < modesNumInput; i++){
    modeInput >> kappas[i] >> modeType[i] >> modeM[i] >> norma[i];
    cout <<"i = "<<i << ", kappa = "<<kappas[i]<<",  modeType ="<<modeType[i]<<", modeM = "<<modeM[i]<<", norma = "<<norma[i]<<endl;
}
func real H(real k, real kp)
{
    return sqrt(k*k-kp*kp);
}
include "axial2D_TEmodes.idp"
include "axial2D_TMmodes.idp"
func complex anE(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{
    int absM = abs(modeNumber-1);
    if(modeType[absM] == 0)
        return anEte(xx, yy, modeNumber, modeM[absM], componentNumber, size1, size2, k);
    else
        return anEtm(xx, yy, modeNumber, modeM[absM], componentNumber, size1, size2, k);
    return 0;
}
func complex anH(real xx, real yy, int modeNumber, int componentNumber, real size1, real size2, real k)
{                       
    int absM = abs(modeNumber)-1;
    if(modeType[absM] == 0)
        return anHte(xx, yy,  modeNumber, modeM[absM], componentNumber, size1, size2, k);
    else
        return anHtm(xx, yy,  modeNumber, modeM[absM], componentNumber, size1, size2, k);
    return 0;
}
func real fNorm(int modeNumber, real size1, real k)
{
    int absM = abs(modeNumber);
    if(modeType[absM-1] == 0)
        return fNormte( modeNumber, size1, k);
    else
        return fNormtm( modeNumber, size1, k);
    return 0;
}
func real Kappa(int modeNumber, real size1, real size2)
{
    int absM = abs(modeNumber);
    if(modeType[absM-1] == 0)
        return Kappate(modeNumber, size1, 0);
    else
        return Kappatm(modeNumber, size1, 0);
    return 0;
}

Finally, the main script. Note that in 2D axial symmetric Maxwell equations (in axial cut) the variable $r E_{\phi}$ is used rather than $E_{\phi}$

load "Element_Mixte"
func complex epsilon(real xx, real yy)
{
     return 1. + 0*1i;
//    if(xx > 0.25 && xx < 0.75 && yy > 0.25 && yy < 0.75) return 5;     else return  1.;
}
real height = 3;
real length = 3;
func mesh generateMesh()
{
    return square(60,30, [x*length, y*height]);
}
mesh Th = generateMesh();
int rightBorderLabel = 2;
int  leftBorderLabel = 4;
include "axial2D_modes.idp"
//plot(Th);

fespace Vh(Th,[RT1Ortho, P2]); // finite element space

func matrix<complex> MakswellEqs(real sigma, int m, real h)
{
	varf MKSWL([Ez,Er, Ephi],[vEz,vEr, vEphi]) =
        int2d(Th)(        
            (
                 (dy(Ephi) - 1i*m*Er )*conj(dy(vEphi)- 1i*m*vEr )/y      //curl_z // vEphi => (Ephi*y)
             +   (dx(Er) - dy(Ez))*conj(dx(vEr) - dy(vEz))*y             //curl_phi
             +   (1i*m*Ez  - dx(Ephi))*conj(1i*m*vEz  - dx(vEphi))/y   //curl_r        
            )    
        -sigma*y*epsilon(x,y)*(conj(vEr)*Er+conj(vEphi)*Ephi/(y*y)+conj(vEz)*Ez)
                 )        
            + on(3,  Ez = 0, Er = 0, Ephi = 0)
            + on(1,  Ephi = 0)                    //Er at the axis does not change anything due to RT1Ortho elements
     ;
    matrix<complex> OP = MKSWL(Vh, Vh, solver=UMFPACK);
    return OP;
}        
func complex[int] vectorBCh(int modeNum, int boundaryLabel, real k)
{
    int m = modeM [abs(modeNum)];
    varf BoundCondRot([Ex,Ey,Ez],[vEx,vEy,vEz]) =
		int1d(Th,boundaryLabel)(
		    (             // x -> z, y ->  r, z -> phi
                anH(x, y, (N.x)*modeNum, 1, height, 0, k)*conj( - N.y*vEz)
              + anH(x, y, (N.x)*modeNum, 2, height, 0, k)*conj(N.x*vEz)
              + anH(x, y, (N.x)*modeNum, 3, height, 0, k)*conj(N.y*vEx - N.x*vEy)*y
                         )*(1i*k)
			       );                                    // [n v*] curl E = [n v*] (i k H)                                                                       
    complex[int] BCr = BoundCondRot(0,Vh);
    return BCr;                        
}    

func complex[int] vectorBCe(int modeNum, int boundaryLabel, real k)
{
    int m = modeM [abs(modeNum)];
    cout<<"modeNum = "<<modeNum<<endl;
    varf BoundCondField([Ex,Ey,Ez],[vEx,vEy,vEz]) =  
	    int1d(Th,boundaryLabel)(
		(                                                     // x(1) -> z, y(2) ->  r, z(3) -> phi;    n [Es Hv]
            2.*pi*conj(
              - (vEz)*anH(x, y, (N.x)*modeNum, 2, height, 0, k)
              + (anE(x, y,  (N.x)*modeNum, 3, height, 0, k))*((-dx(vEz) + 1i*m*vEx) / (1i*k) ) //Ez = anE(..,3,..)*y
              + (vEy) *anH(x, y,  (N.x)*modeNum, 3, height, 0, k) * y  
              - anE(x, y,  (N.x)*modeNum, 2, height, 0, k)*((dx(vEy) - dy(vEx))/(1i*k) * y)
                     )*(N.x)
                   ) /fNorm(modeNum, height, k)
		                  );
    complex[int] BCrf = BoundCondField(0,Vh);
    return BCrf;        
}
func matrix<complex> matrixBC(int modeNum, int boundaryLabel, real k)
{        
    complex[int] BCr  = vectorBCh( modeNum, boundaryLabel,k);
    complex[int] BCrf = vectorBCe( -modeNum, boundaryLabel,k);
    matrix<complex> Br = BCr*BCrf'; // 'cartesian product
    return Br;        
}    

func matrix<complex> generateBCMatrix(int numberOfModes, int boundaryLabel, int sign, real k)
{
    matrix<complex> Br1;
    for(int i = 1; i <= numberOfModes; i++)
    {
        matrix<complex> Br2 = matrixBC(sign*i, boundaryLabel, k);
        Br1 = Br1 + Br2;
    }
    return Br1;        
}    
func complex[int] modeAmplitudes     //complimentary function for calculating scattering parameters
(complex[int]& eVec, int numOfModes, int referenceMode, int inputBoundaryLabel, int otherBoundaryLabel, real k,  bool needdB)
{
    complex[int] result(numOfModes);
    Vh<complex> [ex,ey,ez];
    ex[] = eVec;
    if(needdB) for(int i = 0; i < numOfModes; i++) result(i) = log10(0.);
    complex[int] probe = vectorBCe(-referenceMode, inputBoundaryLabel, k);
    Vh<complex> [pex, pey, pez];
    pex[] = probe;    
    int m = modeM [abs(referenceMode)-1];
    complex power =   eVec'*probe; //'

    for(int testmode = 0; testmode < numOfModes; testmode++)    
    {
        int m = modeM [testmode];
        int modeNum = -(testmode + 1);
        complex tmpPower = 1;
        if(abs(power) != 0) tmpPower = power;

        complex res = int1d(Th,otherBoundaryLabel)((// x -> z, y ->  r, z -> phi;    n [Es Hv]
            2.*pi*y*
            conj(
              - (ez/y)*anH(x, y, modeNum, 2, height, 0, k)                                                                                                            
              + (anE(x, y,  modeNum, 3, height, 0, k))*(-(dx(ez)/y + 1i*m*ex/y) / (1i*k) ) //Ez = anE(..,3,..)*y
              + (ey) *anH(x, y,  modeNum, 3, height, 0, k)
              - anE(x, y,  modeNum, 2, height, 0, k)*((dx(ey) - dy(ex))/(1i*k))
                )*(N.x)
                                                     )
                                                     /(fNorm(modeNum, height, k)*tmpPower));                                                      
         if(needdB) result(testmode) =  20*log10(abs(res));
         else       result(testmode) =  res;
     }

    return result;
}

real sigma = 9.*pi*pi-81.5;
real k = sqrt(sigma);
cout<<"h1 = "<<H(k, Kappa(1,height,1))<<",  kappa1 = "<<Kappa(1,height,1)<<",  k = "<<k<<",  beta_ph = "<<k/H(k, Kappa(1,height,1))<<endl;
cout<<"h2 = "<<H(k, Kappa(2,height,1))<<",  kappa2 = "<<Kappa(2,height,1)<<",  k = "<<k<<",  beta_ph = "<<k/H(k, Kappa(2,height,1))<<endl;
cout<<"h3 = "<<H(k, Kappa(3,height,1))<<",  kappa3 = "<<Kappa(3,height,1)<<",  k = "<<k<<",  beta_ph = "<<k/H(k, Kappa(3,height,1))<<endl;
cout<<"h4 = "<<H(k, Kappa(4,height,1))<<",  kappa3 = "<<Kappa(4,height,1)<<",  k = "<<k<<",  beta_ph = "<<k/H(k, Kappa(4,height,1))<<endl;     


int numberOfModesToAccount = 2;
int targetMode = 1;
matrix<complex> Br = generateBCMatrix(numberOfModesToAccount, rightBorderLabel,1, k);
matrix<complex> Bl = generateBCMatrix(numberOfModesToAccount, leftBorderLabel, 1, k);
matrix<complex> OP = MakswellEqs(sigma, 0, 0) ;

matrix<complex> A;        //A = OP + generateBCMatrix(...) + generateBCMatrix(...) produces
A = OP;                   //order dependent incorrect result tested FreeFem++ v 3.56
A = A + Br;                                                 
A = A + Bl;
complex[int] u(Br.n);
set(A, solver = UMFPACK);
complex[int] RHS =  vectorBCh(targetMode , leftBorderLabel, k);    

u = A^-1*(RHS);    

Vh<complex> [Ex,Ey,Ez];
Ex[] = u;

fespace Uh (Th, P1);
Uh<complex> Ezreal = Ez/(y+1e-10);
Uh<complex> Exnorm = Ex;

plot(Ex, fill = true, cmm = "EX NORM");
plot(Ey, fill = true, cmm = "EY");     
plot(Ezreal, fill = true, cmm = "EZ");

cout<<    modeAmplitudes(u, numberOfModesToAccount, -targetMode,  leftBorderLabel,  rightBorderLabel, k, false)<<endl;
cout<< modeAmplitudes(u, numberOfModesToAccount, -targetMode, leftBorderLabel, leftBorderLabel, k, false)<<endl;

Validation

Following examples show reflectiveless transition of a waveguide mode traveling from one port (left) to an other (right).

2D, Cartezian

Left and right borders are waveguide ports. Input mode TE1

Mode TE1, abs(Ez)

Mode TE1, Re(Ez)

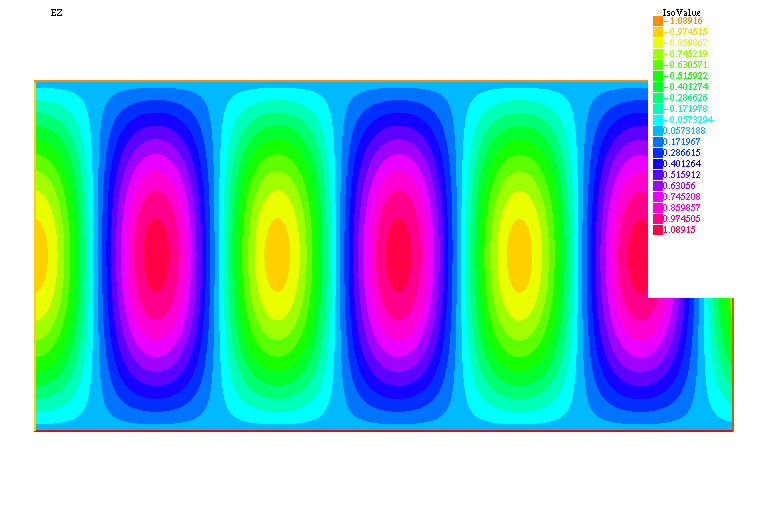Left and right borders are waveguide ports. Input mode TM1

Mode TM1, abs(Ex)

Mode TM1, abs(Ey)

2D, axial-symmetric

Mode TE01, abs(Ephi)

Mode TE01, Re(Ephi)

Mode TM02, abs(Ez)

Mode TM02, abs(Er)

Author

Petr Makhalov