Stokes
Algorithms for solving the 2D and 3D static Stokes equations
Problem
Solve:
\[\left\{ \begin{align*} -\mu\Delta\mathbf{u} + \nabla p &= 0\\ \nabla\cdot\mathbf{u} &= 0 \end{align*} \right.\]Variational form
$ \displaystyle{ \mu\int_{\Omega}{\nabla\mathbf{u}:\nabla\mathbf{v} - p\nabla\cdot\mathbf{v}} - \int_{\partial\Omega}{\left(\mu\frac{\partial\mathbf{u}}{\partial\mathbf{n}}-p\mathbf{n}\right)\cdot\mathbf{v}} = \int_{\Omega}{\mathbf{f}\cdot\mathbf{v}} } $
$ \displaystyle{ \int_{\Omega}{\nabla\cdot\mathbf{u}q} = 0 } $
Stabilisation term:
$ \displaystyle { \int_{\Omega}{\varepsilon p q} } $
Algorithms
2D
Poiseuille flow in a pipe
//Parameters
real uMax = 10.;
real Mu = 1.;
func fx = 0.;
func fy = 0.;
//Mesh
int nn = 10; //Mesh quality
real L = 5.; //Pipe length
real D = 1.; //Pipe height
int Wall = 1; //Pipe wall label
int Inlet = 2; //Pipe inlet label
int Outlet = 3; //Pipe outlet label
border b1(t=0., 1.){x=L*t; y=0.; label=Wall;};
border b2(t=0., 1.){x=L; y=D*t; label=Outlet;};
border b3(t=0., 1.){x=L-L*t; y=D; label=Wall;};
border b4(t=0., 1.){x=0.; y=D-D*t; label=Inlet;};
int nnL = max(2., L*nn);
int nnD = max(2., D*nn);
mesh Th = buildmesh(b1(nnL) + b2(nnD) + b3(nnL) + b4(nnD));
//Fespace
fespace Uh(Th, [P2, P2]);
Uh [ux, uy];
Uh [vx, vy];
fespace Ph(Th, P1);
Ph p;
Ph q;
//Macro
macro Gradient(u) [dx(u), dy(u)] //
macro Divergence(ux, uy) (dx(ux) + dy(uy)) //
//Function
func uIn = uMax * (1.-(y-D/2.)^2/(D/2.)^2);
//Problem
problem S ([ux, uy, p],[vx, vy, q])
= int2d(Th)(
Mu * (
Gradient(ux)' * Gradient(vx)
+ Gradient(uy)' * Gradient(vy)
)
- p * Divergence(vx, vy)
- Divergence(ux, uy) * q
)
- int2d(Th)(
fx*vx + fy*vy
)
+ on(Inlet, ux=uIn, uy=0.)
+ on(Wall, ux=0., uy=0.)
;
S;
//Plot
plot(p, cmm="Pressure");
plot([ux, uy], cmm="Velocity");| Result - velocity (top) and pressure (bottom) |
|---|
 |
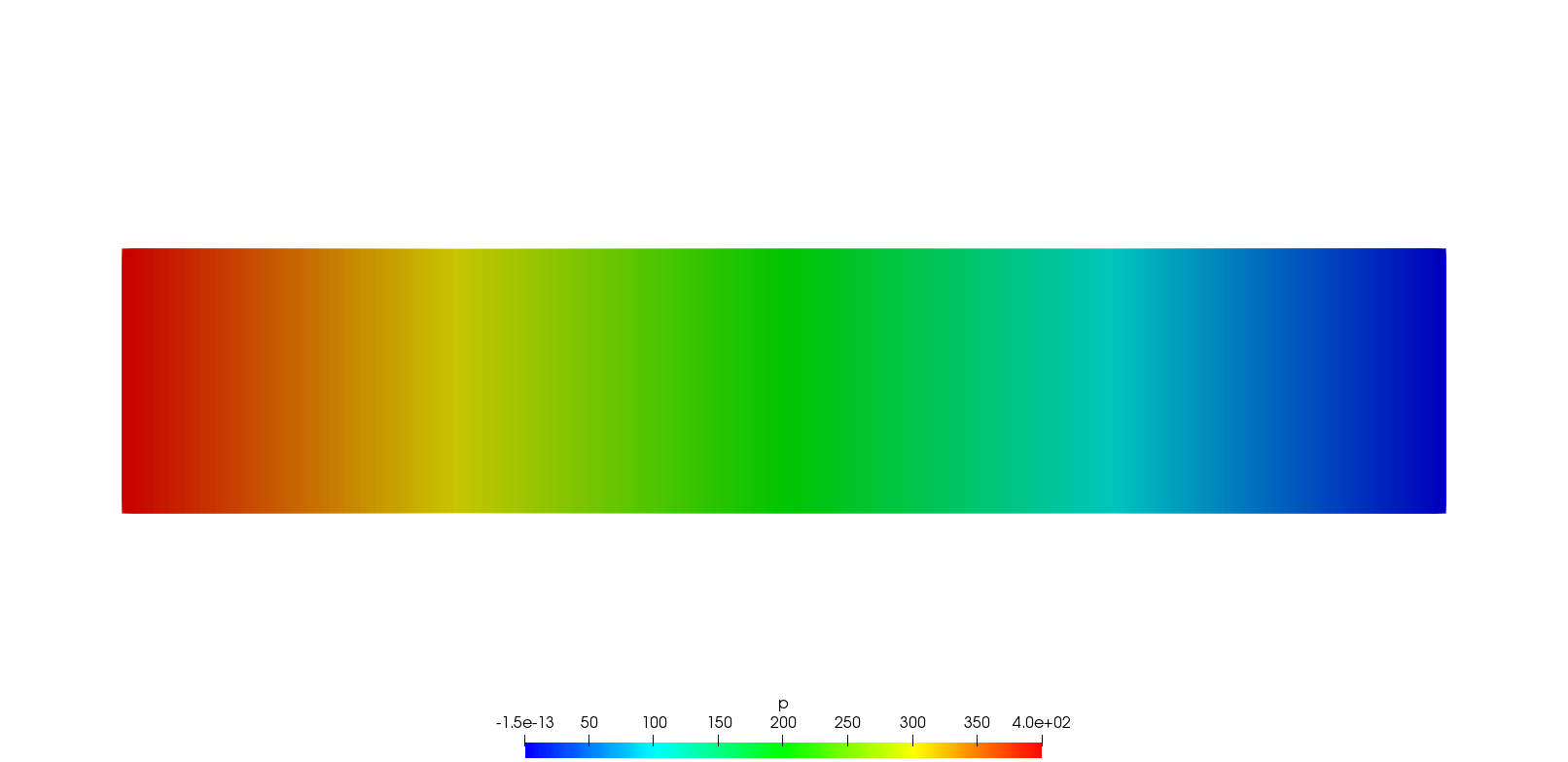 |
3D
Poiseuille flow in a pipe
load "msh3"
//Parameters
real uMax = 10.;
real Mu = 1.;
func fx = 0.;
func fy = 0.;
func fz = 0.;
//Mesh
int nn = 5; //Mesh quality
real L = 5.; //Pipe length
real D = 1.; //Pipe diameter
int Wall = 1; //Pipe wall label
int Inlet = 2; //Pipe inlet label
int Outlet = 3; //Pipe outlet label
real R = D/2.;
border b0(t=0., 2.*pi){x=R*cos(t); y=R*sin(t); label=0;};
int nnL = max(2., L*nn);
int nnR = max(2., 2.*pi*R*nn);
mesh Th0 = buildmesh(b0(nnR));
int[int] ldown = [0, Inlet];
int[int] lmid = [0, Wall];
int[int] lup = [0, Outlet];
mesh3 Th = buildlayers(Th0, nnL, zbound=[0., L], labeldown=ldown, labelmid=lmid, labelup=lup);
//Fespace
fespace Uh(Th, [P2, P2, P2]);
Uh [ux, uy, uz];
Uh [vx, vy, vz];
fespace Ph(Th, P1);
Ph p;
Ph q;
//Macro
macro Gradient(u) [dx(u), dy(u), dz(u)] //
macro Divergence(ux, uy, uz) (dx(ux) + dy(uy) + dz(uz)) //
//Function
func uIn = 1.-(x^2+y^2)/R^2;
//Problem
problem S ([ux, uy, uz, p],[vx, vy, vz, q])
= int3d(Th)(
Mu * (
Gradient(ux)' * Gradient(vx)
+ Gradient(uy)' * Gradient(vy)
+ Gradient(uz)' * Gradient(vz)
)
- p * Divergence(vx, vy, vz)
- Divergence(ux, uy, uz) * q
)
- int3d(Th)(
fx*vx + fy*vy + fz*vz
)
+ on(Inlet, ux=0., uy=0., uz=uIn)
+ on(Wall, ux=0., uy=0., uz=0.)
;
S;
//Plot
plot(p, cmm="Presure");
plot([ux, uy, uz], cmm="Velocity");| Result - velocity (top) and pressure (bottom) |
|---|
 |
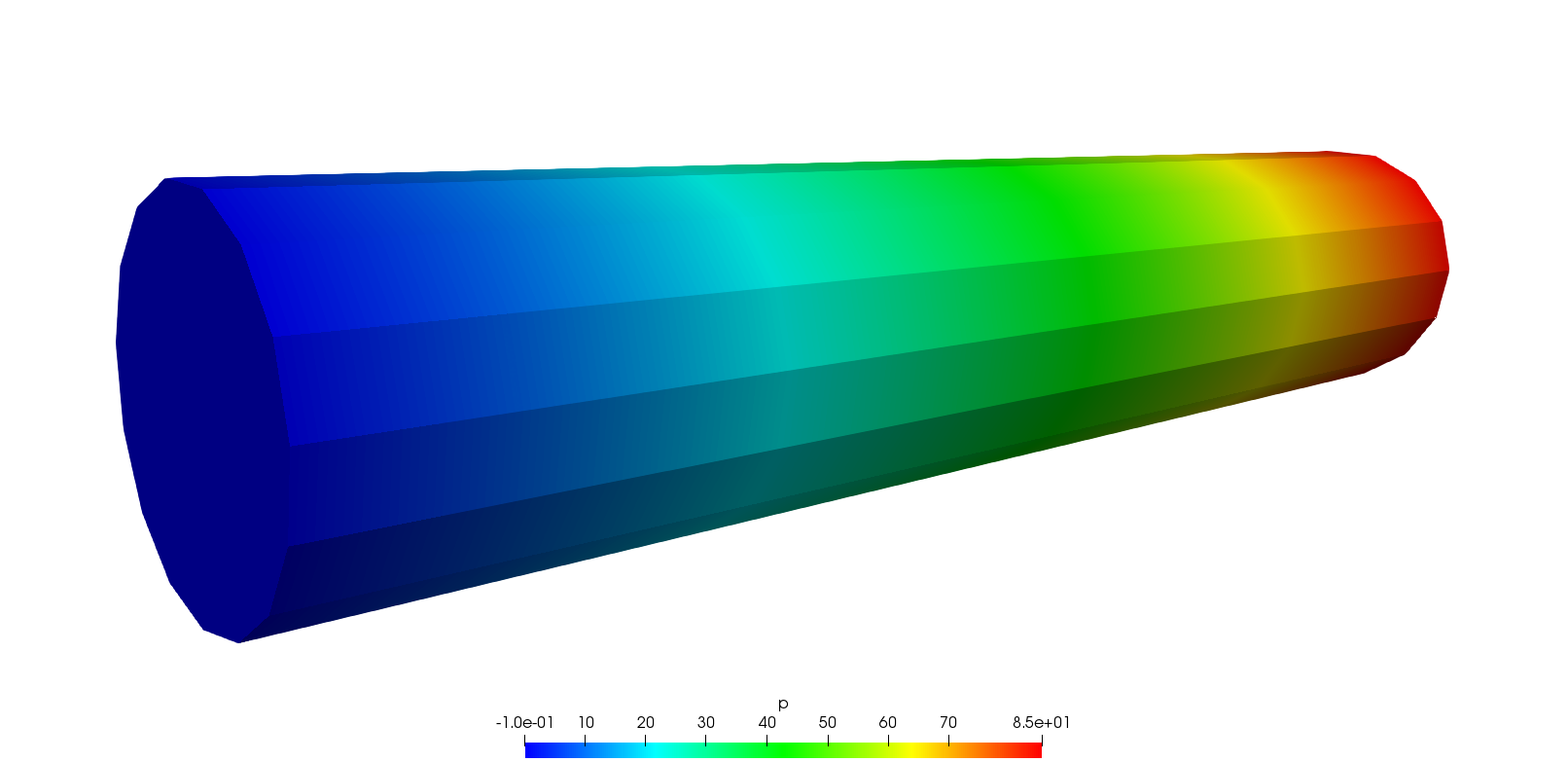 |
Authors
Author: Simon Garnotel
